That is the decomposition is unique to within a scalar multiple. Click now to know about the different matrices with examples like row matrix column matrix special matrices etc.
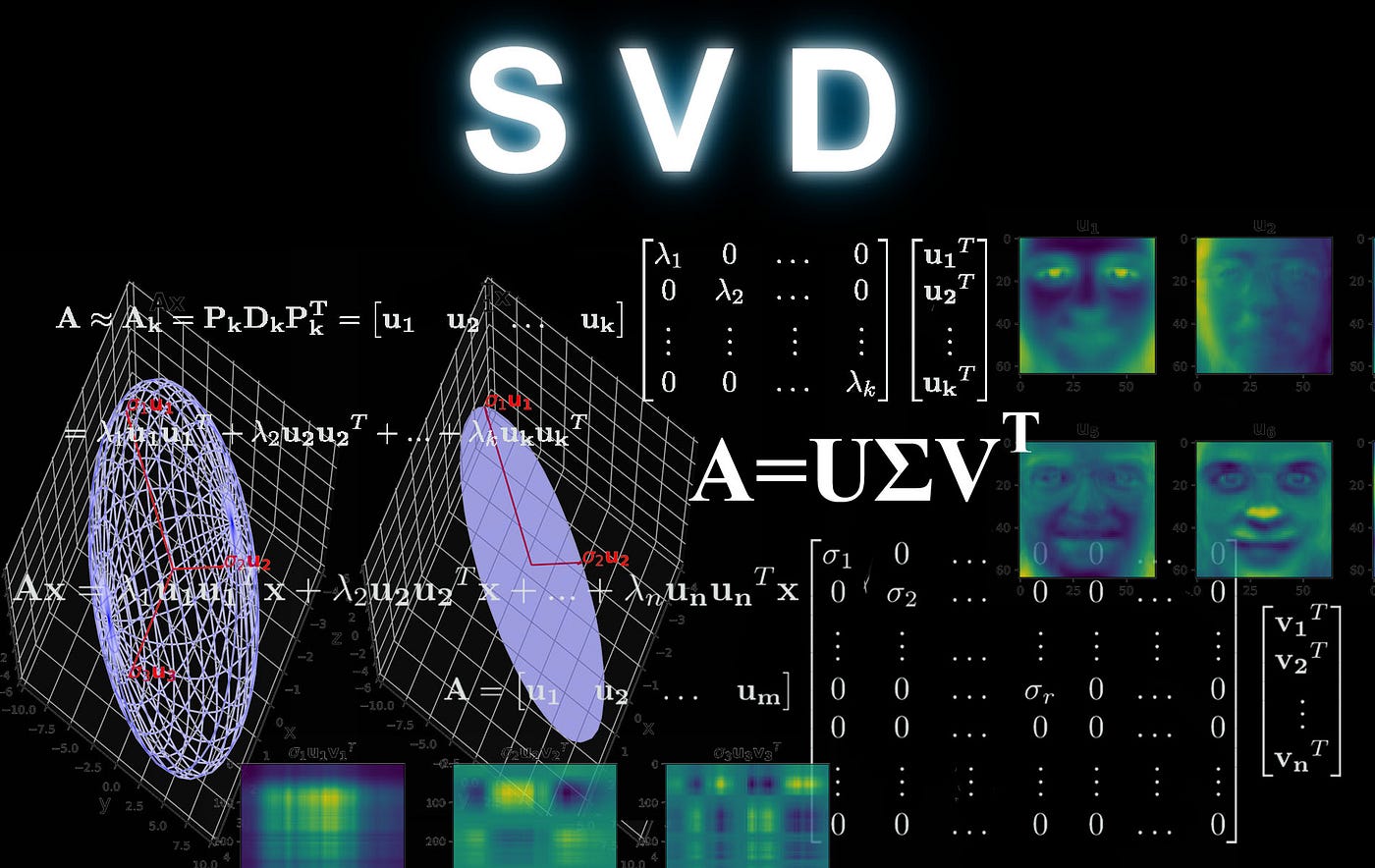
Understanding Singular Value Decomposition And Its Application In Data Science By Reza Bagheri Towards Data Science
Iconic Shiksha Properties Of Rank Of Matrix Facebook

What Can We Find From Rref Hungyi Lee
Inverse Matrix Inverse Matrix is an important tool in the mathematical worldIt is used in solving a system of linear equations.

Properties of rank of matrix. If Axy T is a rank-one matrix then If Apq T then pkx and qyk for some scalar k. The dimension of the linear space. Computes the sign and natural logarithm of the absolute value of the determinant of a square matrix.
If we consider a square matrix the columns rows are linearly independent only if the matrix is nonsingular. Rank of a matrix A is denoted by ρA. The rank of a null matrix is zero.
In other words the rank of any nonsingular matrix of order m is m. Computes the numerical rank of a matrix. Definition 111 Matrix A rectangular array of numbers is called a matrix.
Computes the condition number of a matrix with respect to a matrix norm. There is an n-by-n matrix B such that AB I n BA. Types of Matrices - The various matrix types are covered in this lesson.
The rank of a matrix cannot exceed the number of its rows or columns. Computes the determinant of a square matrix. A non-zero matrix A is a rank-one matrix iff it can be decomposed as Axy T.
It plays in matrix multiplication the same role played by 1 in the multiplication of numbers. The rank cant be larger than the smallest dimension of the matrix. Inverse matrices are frequently used to encrypt or decrypt message codes.
The following statements are equivalent ie they are either all true or all false for any given matrix. William Ford in Numerical Linear Algebra with Applications 2015. Let A be a square n by n matrix over a field K eg the field R of real numbers.
The rank of a circulant matrix is equal to where is the degree of the polynomial. A matrix having mrows and ncolumns is said to have the order m n. For a 24 matrix the rank cant be larger than 2.
What are the Properties of an Invertible Matrix. It is also used to explore electrical circuits. An invertible matrix in linear algebra also called non-singular or non-degenerate is the n-by-n square matrix satisfying the requisite condition for the inverse of a matrix to exist ie the product of the matrix and its inverse is the identity matrix.
The matrix A has a left inverse that is there exists a B such that BA I or a right inverse that is. How to multiply a matrix by a scalar definition and properties of scalar multiplication. The rank of a matrix is the dimension of the subspace spanned by its rows.
Computes a matrix norm. Any circulant is a matrix polynomial namely the associated polynomial in the cyclic permutation matrix. We shall mostly be concerned with matrices having real numbers as entries.
Rank of a matrix. When the rank equals the smallest dimension it is called full rank a smaller rank is called rank deficient. If Axy T is a square rank-one matrix then A has a single non-zero eigenvalue equal to x T yy T x.
Properties The invertible matrix theorem. And download free types of matrices PDF lesson. As we will prove in Chapter 15 the dimension of the column space is equal to the rankThis has important consequences.
For instance if A is an m n matrix and m n then rank A n but if m n then rank A m. The horizontal arrays of a matrix are called its rowsand the vertical arrays are called its columns.

Gate Ese Rank Of Matrix In Hindi Offered By Unacademy
1

Solved Problem 2 Let A Be An N X K Matrix And K S N And Chegg Com
Virtual Gate Test Series Linear Algebra Rank Of The Matrix Gate Overflow

Gate Ese Rank Of Matrix And Properties In Hindi Offered By Unacademy

Solved Problem 2 2 Assume P N And Let X E Rnxp Be A Chegg Com
Rank Of

Linear Algebra For Machine Learning Part 5 Singular Value Decomposition Svd And Matrix Pseudo Inverse By Falguni Mukherjee Medium

